After a wonderful year of living in Munich and working at the Institute for Plasma Physics there, I decided to return to my first love: dense, magnetised plasmas. Since April 1st I’ve been working again as a post doc at Imperial College London, in the MAGPIE Group. Of course, this has all been remote work due to the ongoing epidemic, but despite being an experimental physics group, we’ve managed to keep pretty busy. This post is quick overview of what I’ve been doing, maybe in part to convince myself I’ve actually achieved something in the last two months.
Thomson Scattering
By far the most popular diagnostic we field is Thomson Scattering, and it’s not hard to see why. For our plasmas, it is a non-perturbative, local measurement of velocity, temperature and even density, which is a good amount of the parameters in a plasma. There are even recent papers using Thomson to measure the local electric current, which means you can infer the magnetic field – that’s a full house!
The Thomson analysis code our group uses was written by me in a great hurry in the middle of my PhD. It is far from perfect, and bits keep going wrong when people try to analyse data which doesn’t look exactly like the data I was analysing – this is a pretty constant feature of most scientific code. Since I’ve been back I’ve been fixing a fair few bugs and errors, including one particularly nasty one to do with convolution which shifted our signal, creating a fake Doppler shift of around 5 km/s – pretty speedy, though fortunately not that speedy compared to the speeds of 50 km/s we usually measure.
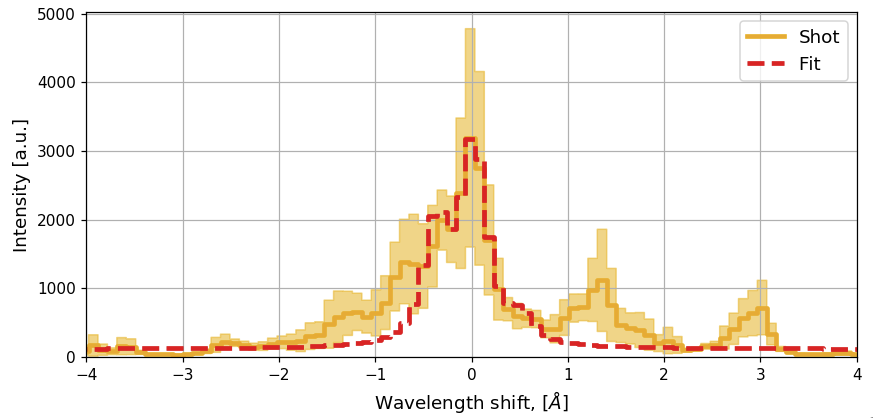
In addition, I was inspired by a recent paper to find a better way to handle the uncertainties in our spectra. We calculate the spectra by averaging over several rows on our CCD, and so there is enough information there to work out the standard deviation per column, which represents a bin centered on a wavelength. The tricky bit is correcting for the fact that the intensity varies across the rows due to the coupling from the fibre optic bundle. I found a way to correct for this which seems to work well, and now we have uncertainties for each spectra. Not only does this make for nice plots, but it also allows us to weight our fitting routine with the inverse of the uncertainties, so the routine knows to care less about points which are more uncertain. This leads to better fits, so what’s not to like.
Faraday Woes
Significantly less successful has been my attempt to understand some of the woes besetting our Faraday Rotation Imaging diagnostic. Here we image the rotation angle of the linear polarisation of a laser beam which passes through the plasma. This rotation angle should be proportional to the line integral of the product of the electron density and the magnetic field component along the laser beam.
We use a differential measurement consisting of a beam splitter which sends light to two cameras which have polarisers at the angle from extinction, but in different directions. Hence if the magnetic field points in one direction in a region of the image, that region will show up brighter on one camera, and darker on the other, as the polarisation is rotated towards extinction on one, and away from extinction on the other.
That’s the idea, but in the last year or so that hasn’t been working so well. many ideas have been proposed, such as damaged coatings on optics from the high powered laser, an elliptical component of the polarisation or issues with the extinction ratios of the polarisers. Two of the MAGPIE PhD students made some exhaustive (and doubtless exhausting) measurements using a half wave plate to simulate the plasma (this rotates the angle of linear polarisation) and I had thought by analysing all this data I could put together a consistent picture.
Alas, it was not to be. All I’ve really found is that we could do with some simple, stripped down experiments, which we can’t do until we can get back into the lab. So watch this space.
Synthetic Diagnostics
I’ve also been working with MAGPIE’s newest PhD student, Stefano Merlini, to model a new diagnostic we’ve been developing to study density fluctuations in turbulent plasmas. This project has two main components: firstly, generating turbulent fields with a specified power-law index, and then tracing photons through this field to see what a laser beam would look like after traversing such a plasma.

For the first part, we’re working with Archie Bott at Princeton, who is providing the serious theoretical brains, and for the second part with Jerry Chittenden’s group at Imperial College, who have the numerical skills to trace thousands of photons through a very messy plasma. Our part is putting these together, and working out what we as experimentalists can measure.
It’s odd working remotely, especially as I’ve never met Stefano in person, but it’s a very fun project and it gets me thinking a lot about turbulence.