What a long post. There is a bit about dragons at the end!
This is the rather grandiose title that Lindemuth and Siemon give their paper. The authors want to draw a map of what possible reactors would look like. Then they want to use this map to find a reactor that looks easy to build and economically viable to operate. The authors are particularly interested in why the two major approaches to nuclear fusion use plasmas that are such different sizes and densities.

ITER (left) is huge – you can a scale person in blue at the bottom. In contrast, NIF (right) uses tiny fuel pellets, only 2mm in diameter, though the infrastructure that surrounds the pellet is still very large.
I’m currently rereading it as I’m writing my ‘transfer report’, a document for which I have no brief, but vaguely believe to be part literature review and part research proposal.
Unfortunately, most people will be unable to access the paper as it’s behind a paywall. I haven’t yet found a legal looking free version. The authors claim that
“Our intent is to provide a simple quantitative introduction to fusion research that is suitable for an introductory class on fusion.”
and they’re quite successful, though it’s definitely a paper that’s easier to read after some exposure to plasma physics and nuclear fusion.
Their analysis is straightforward. They assume a zero dimensional plasma, which is the same as saying the density and temperature and all other parameters are constant throughout the plasma. This isn’t realistic, real plasmas will have different temperatures and densities at different points. However, this simplifying assumption does allow the authors to write down some simple equations for the fusion power output from a 50:50 Deuterium:Tritium plasma in terms of only its density and temperature.
Next, the authors consider the energy losses from the plasma. These could be from it emitting light and cooling (think how a toaster loses energy by glowing red hot) or because hot particles leave the plasma. In order to produce net energy, the energy losses must be less than the energy produced by fusion reactions. For an economically viable reactor, the energy produced should substantially exceed the losses.
With this condition, the authors begin to estimate some physical parameters of a fusion device. For example, given some density and temperature, how big must the reactor be? How much energy needs to be used to heat the fuel? This gives some idea of how feasible a reactor could be – for some densities and temperatures, the reactor would need to be thousands of metres in diameter, and you’d need to put in all the daily energy received from the Sun to get the reactor going – this reactor isn’t likely to be built any time soon!
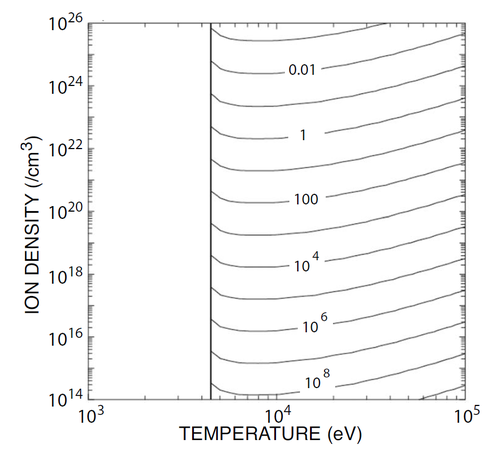
Reactor size in cm for a range of densities and temperatures. The black lines show constant reactor size, so you can roughly see that the size doesn’t changed much as the temperature changes, but does change a lot as the density changes. 1 ev is about 10,000K. From [1].
At this point, the authors haven’t considered a magnetic field. As I discussed before, magnetic fields stopped charged particles from wandering all over the place, and so a strong magnetic field can prevent energy being lost from the plasma by stopping hot particles from leaving.
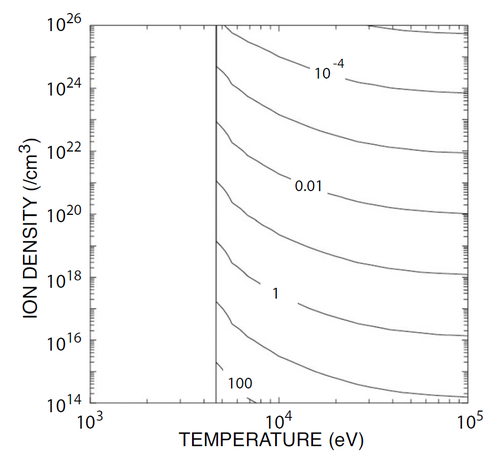
System size in cm for a range of densities and temperatures when a strong magnetic field is applied. 1 ev is about 10,000K. From [1].
Now, it would be nice here to have three parameters – the density of plasma, the temperature of the plasma, and the magnetic field in the plasma. But it’s hard to draw graphs with three parameters all changing, so instead the authors set the magnetic field so that the magnetic pressure equals the thermal pressure. Thermal pressure is a concept everyone is familiar with – it’s the pressure in your bicycle tyres, or in the air around you.
Magnetic pressure is slightly odder. Because magnetic fields only act on charged particles, humans (who are neutrally charged) don’t experience magnetic pressure. But charged particles can be pushed around very strongly by magnetic fields, and so if the magnetic field is stronger on one side of a charged particle than the other, than the particle will move towards the region with lower magnetic pressure. This is the same as molecules in the air moving from a higher pressure to a lower pressure region, something anyone who has had a sudden tyre puncture will be familiar with!
So now we get to the interesting part of the paper. We have a map, and we want to find a good reactor. The authors point out that the two major paths to a fusion reactor that are currently being studied lie in opposite corners of the map. The region in the middle has been mostly ignored, both in terms of theory and experiments. So like Columbus positing that a quick route to the East might be possible if you sail West*, the authors propose looking in the ‘here be dragons’ region for a viable fusion reactor.
Image from Wikipedia
It turns out there are some interesting concepts that lie in this unexplored region. Using a strong magnetic field and mid-range densities looks quite promising on paper. One of the concepts is MagLIF, which I’ve written about before. However, much like the tales of Eldorado, we should be cautious about getting too excited over the unknown – a lot of work needs to be done to see whether these densities and temperatures will yield a working fusion reactor. So much of the fundamental physics is unknown, and quite tricky to model – the magnetic pressure doesn’t dominate over the thermal pressure, so we can’t neglect either pressure when doing calculations.
The paper ends with some rather suspect calculations of the cost of reactor following this ‘third way’, and I think it’s by far the weakest point – not only does it come up with numbers which are absurdly low ($50 million for a reactor?) the authors use very few data points (just the cost of NIF and ITER, which typify the other two reactor pathways) to reach their conclusions.
Still, it’s remarkable how much understanding can be gained by simple mathematics and some stripped down physics. Whilst we still need powerful computer simulations and rigorous experiment to be accurate, it’s really nice to be able to get a rough overview without all of that effort!
*Is this apocryphal? I have no idea. But you get the point – look in unexplored places for exciting things.
[1] Irvin R. Lindemuth and Richard E. Siemon ‘The fundamental parameter space of controlled thermonuclear fusion’ Am. J. Phys. 77, 407 (2009); http://dx.doi.org/10.1119/1.3096646