In my last blog post I discussed measuring the temperature of a plasma. I talked about firing an intense laser into the plasma and looking at the light that is reflected off the plasma using a spectrometer. A spectrometer measures the spectrum (think ‘colour’) of the reflected light, and from the range of wavelengths in the spectrum we can deduce the temperature of the plasma.
The description I gave last time is appropriate when the wavelength of the laser light is smaller than the shortest distance over which the plasma can respond to electric fields. That probably doesn’t make much sense, so consider an analogy.

By Fæ CC BY-SA 3.0 via Wikimedia Commons
Think about a large, crowded street. If you focus on one person, their motion seems random, constantly stopping and changing direction, without a clear purpose. If you broaden your focus a little bit, you see more people – maybe couples walking together, or a group of friends or a coach tour. These groups act collectively, and our individual person must step out of the way or squeeze past other individuals and groups – this explains the odd behaviour that we puzzled over when we could only see one person. On an even larger scale, we see flows of people, up and down the street, with sinks and sources at shop doorways or side streets. At this level, the behaviour of the individuals on the street is unimportant – we can say the behaviour of the crowd is due to ‘collective motion’ which doesn’t necessarily look like the random, individual motion on smaller scales.
Plasmas are similar. On different length scales, different processes are important. In a plasma there is a fundamental length scale called the Debye length, which is the distance over which electric fields are reduced to zero by the collective motion of the charged particles in the plasma. For reflected light of wavelengths shorter than the Debye length, the light reveals information on the individual motion of charged particles. At wavelengths longer than the Debye length we get information on the collective motion of the particles.
I’ve already discussed the result due to individual motion measured by a short wavelength laser in my previous blog post. The light, which is initially all at one wavelength, becomes smeared out by the Doppler shift as all the electrons are moving randomly towards or away from the laser. It is possible to deduce the electron temperature by the range of wavelengths recorded because the temperature is directly linked to the random velocities of the electrons.
More interestingly, we can consider the result for collective motion, using a longer wavelength laser. For almost all of the plasmas we study on MAGPIE the Debye length is about the same as the wavelength of the laser we have, so we are on the boundary between measuring collective and individual motion. What sorts of collective motion are there in a plasma? Despite the convincing analogy above, I don’t expect you to believe there are couples and tour groups inside a plasma, but instead we have sound waves. A ‘wave’ here means the physicists’ short hand for a propagating disturbance, and sound waves are propagating disturbances of density and pressure.
Sound waves in a plasma are similar to sound waves in air – they move at a fixed speed determined by the temperature of the air and the mass of the air molecules, and inside a sound waves the particles oscillate backwards and forwards without an bulk motion. Sound waves can exist inside a moving plasma just as they can inside moving air (you can, afterall, have a conversation in a car). When our laser reflects off particles which are being oscillated by a sound wave, it will see an equal number moving away from the laser as towards – this gives rise to two peaks in the spectrum of the reflected light, space evenly on either side of the original wavelength. The two peaks correspond to the reflected light being Doppler shifted to both higher and lower frequencies by the particles moving towards and away from the laser.
Because the velocity of the sound waves is known and depends only on the plasma temperature and the mass of the charged particles, we can determine the plasma temperature from the frequencies at which the peaks occur. To be more precise, the sound speed in a plasma depends on the electron temperature but the mass of the ions – as electrons and ions in a plasma can have quite different temperatures this is quite interesting.
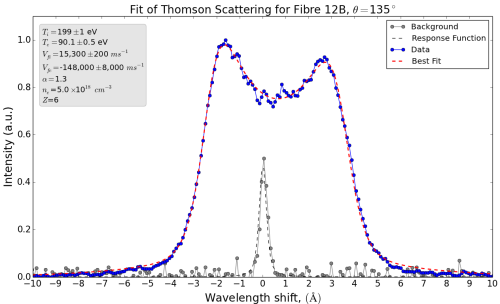
Two peaks due to sound waves in a carbon plasma, measured on MAGPIE. The two peaks are at different heights due to an effect called Electron Landau Damping, which I can’t think how to explain right now – this probably means I don’t understand it. Fortunately for us, it turns out to be a useful measure of another important plasma property, the relative speed of the electrons with respect to the ions.

By pam fray CC BY-SA 2.0, via Wikimedia Commons
In a plasma with a magnetic field, there is yet another type of wave. This arises because charged particles spiral around magnetic field lines, a concept I discussed in one of my first blog posts. Think about a Merry-go-round with someone on every horse.. As the merry-g-round spins, some of the people are coming directly towards you, some directly away, and the rest are going left or right or some mix of all of these. Because you are looking from the side, there appear to be more people heading directly towards or away from you than there are going left or right.
In a plasma, if you look at right angles to the magnetic field line, you will analogously see more charged particles moving directly towards or away from you, and so light reflected from a plasma with a magnetic field will have peaks corresponding to the collective motions of the particles [1].
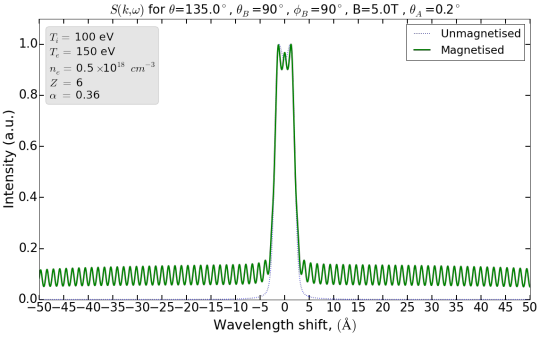
Spectrum of light scattered from a plasma with magnetised electrons. Own work. The tall peaks due to the sound waves are in the middle – the smaller peaks out to the sides are due to the magnetic field.
In fact, you don’t just see two peaks, but huge range of peaks. I can’t explain why there are so many using the basic picture I’ve outlined above. I would have to mutter something about non-linearity and harmonics, but that wouldn’t convince me either. If I find a good explanation I’ll write a blog post about it – at the moment I simply rely on the mathematics.
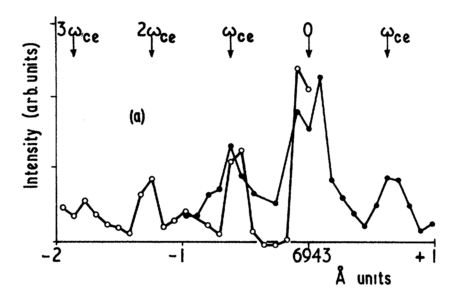
Data from Evans et al. [2] – peaks due to collective motion of the plasma’s electrons in a magnetic field.
However, I can say that the peaks all equally spaced by a wavelength that depends only on the magnetic field and the mass of the electron. As such, this is a remarkably sensitive and precise technique for measured magnetic fields, but the last time I can find that it was done experimentally was in 1970 [2]. I’d very much like to try this experiment in MAGPIE, but it requires very precise alignment of the laser and the spectrometer, so it may elude us. Congratulations on getting to the end of this blog post – have some references:
[1] Froula, D., Luhmann, N., Sheffield, J., & Glenzer, S. (2011). Plasma scattering of electromagnetic radiation.
[2] Evans, D. E., & Caolan, P. G. (1970). Measurement of magnetic field in a laboratory plasma by Thompson scattering of laser light. Physical Review Letters, 25(23), 1605–1608.